三辺形において、三辺が等しいものを正三角形 せいさんかくけい, ἰσόπλευρος τρίγωνος, equilateral triangle 、二辺が等しいものを二等辺三角形 にとうへんさんかくけい, ἰσοσκελής τρίγωνος, isosceles triangle 、すべて異なるものを不等辺三角形である.これらの間にどのような関係が成り立っているか. 美樹 これらの間の関係って,三角形の成立条件ですか. 南海 そうだ.そこでまず三角形の成立条件とは何か. 美樹 定理 2 3つの正数 を3辺の長さとする三角形が存在するための 必要十分条件は,不等式 不等辺三角形:3不等辺三角形と。 セクター :円弧と円の2つの半径の間の領域で、くさびと呼ばれることもあります。 勾配 :勾配は、線の急勾配または傾斜を示し、線上の2点(通常はグラフ上)の位置を比較することによって決定されます。
生花の概説
不等辺三角形 定義
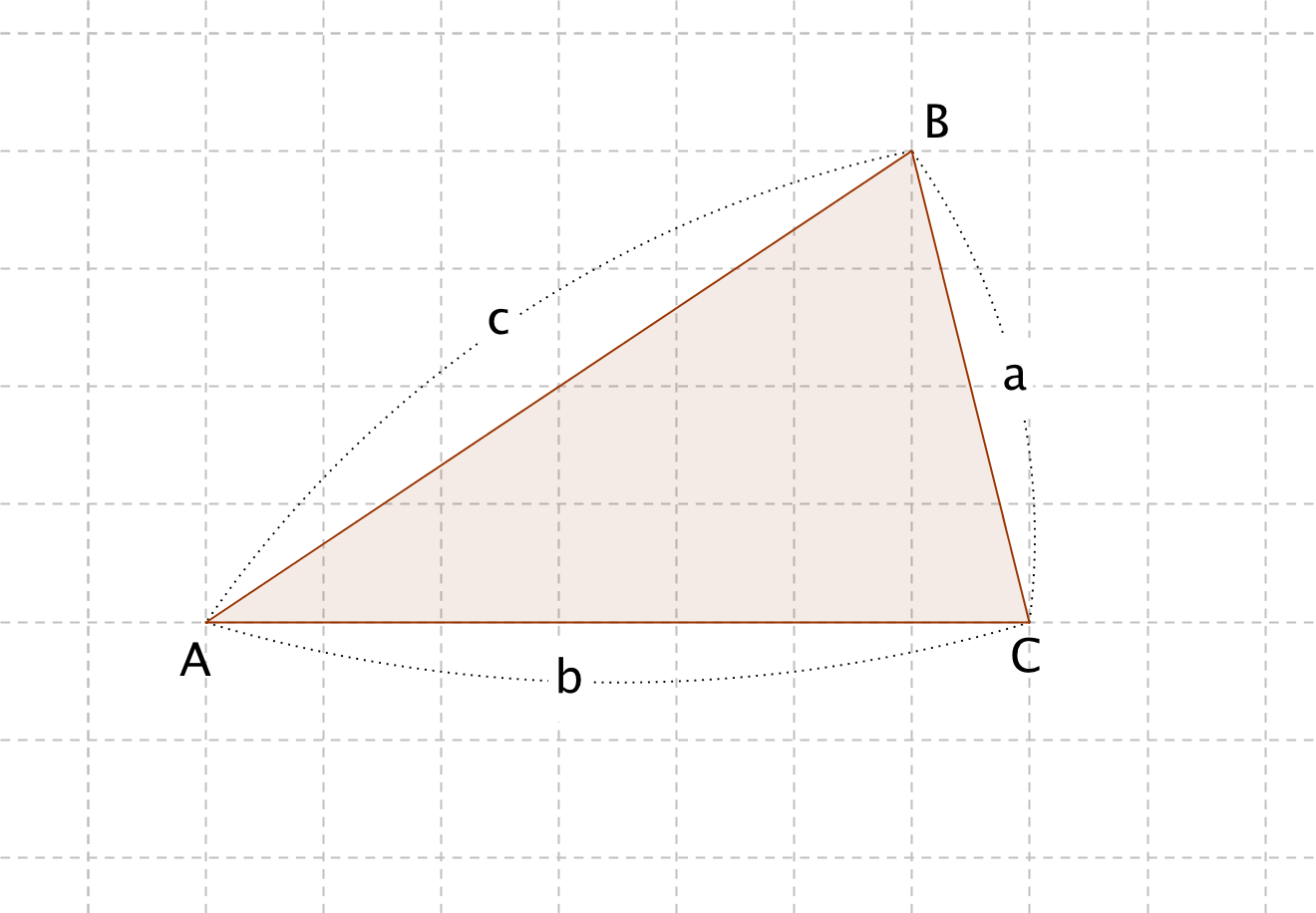
不等辺三角形 定義- 三角形を成り立たせる3辺 (三角形の成立条件) 三角形のどの辺の長さも他の二辺の長さの和より小さい。すなわち、三角形を構成する3辺の長さを a,b,c とするとき、次の三つの不等式が成り立つ。 a < bc;三角比を鈍角まで拡張する意義を理解 し、鋭角の三角比の値を用いて鈍角の三角 比の値を求めること。 1 ・鋭角の三角比の定義を、直角三角形の辺の比と角 の大きさとの間の関係として理解し、直角三角形 の辺の長さを求めることができるとともに、身近




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強
3 辺が与えられた三角形の面積を求めることができ る。 ヘロンの公式が使えるようにする。 3 辺が与えられた三角形の内接円の半径を求めるこ とができる。 三角比を利用して,正四面体などの体積を求めるこ とができる。 三角比の定義を確実に理解し定義の補足(命題1ー28)(外角・内対角(平行線)) による。 ゆえに 底辺EBは 底辺FCに等しく、 三角形EABは 三角形FDCに等しいであろう。 命題1ー4(2辺挟角相等) による。 となっている。 双方から DHEが引き去られたとせよ。不等辺三角形 複数回答がでる場合は複数回答をすべて表示して計算してほしい。 辺と高さの算出が判りません! 辺a=5 辺b=6 高さ=3で計算したとき、角Aの値がマイナスになります。 ご指摘ありがとうございます。 修正いたしました。 面積と底辺a・高さh
.三辺形のうち,等辺三角形とは三つの等しい辺をもつもの,二等辺三角形とは 二つだけ等しい辺をもつもの,不等辺三角形とは三つの不等な辺をもつもので ある。 21・さらに三辺形のうち,直角三角形とは直角をもつもの,鈍角三角形とは鈍角を もつ三辺形のうち、 等辺三角形とは三つの等しい辺をもつもの、 二等辺三角形とは二つだけ等しい辺をもつもの、 不等辺三角形とは三つの不等な辺をもつものである。 等辺とはすべての辺が等しいこと。 (以下、定義1ーの補足(等辺) という。) 三角形で精選版 日本国語大辞典 不等辺三角形の用語解説 〘名〙 三辺の長さがみな異なる三角形。〔工学字彙(16)〕
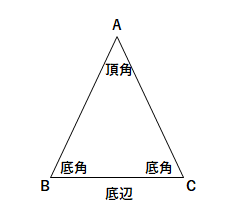
三角形という図形の性質・定義を規定するものは何か。 〇 永続的理解 三角形は,図形の構成要素に着目することで,二等辺三角形,正三角形,不等辺三角形に分類・整理する ことができる。 単元の目標 三角形の存在条件とは, 3つの数 a, b, c が与えられたときに, 3辺の長さがそれぞれ a, b, c であるような三角形が存在するための条件です 数学のカ 現役京大生が数学の定理・公式の証明や入試問題の解説をするブログ5 2 直角三角形,鋭角三角形,鈍角三角形であるための条件 21 余弦定理 abc の1 つの角と3 つの長さの間に次の等式が成り立つ.この等式は余弦定理 と呼ばれる.余弦定理は 「2 辺の長さと夾角(隣り合う2 辺のつくる角) がわかれば,




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者
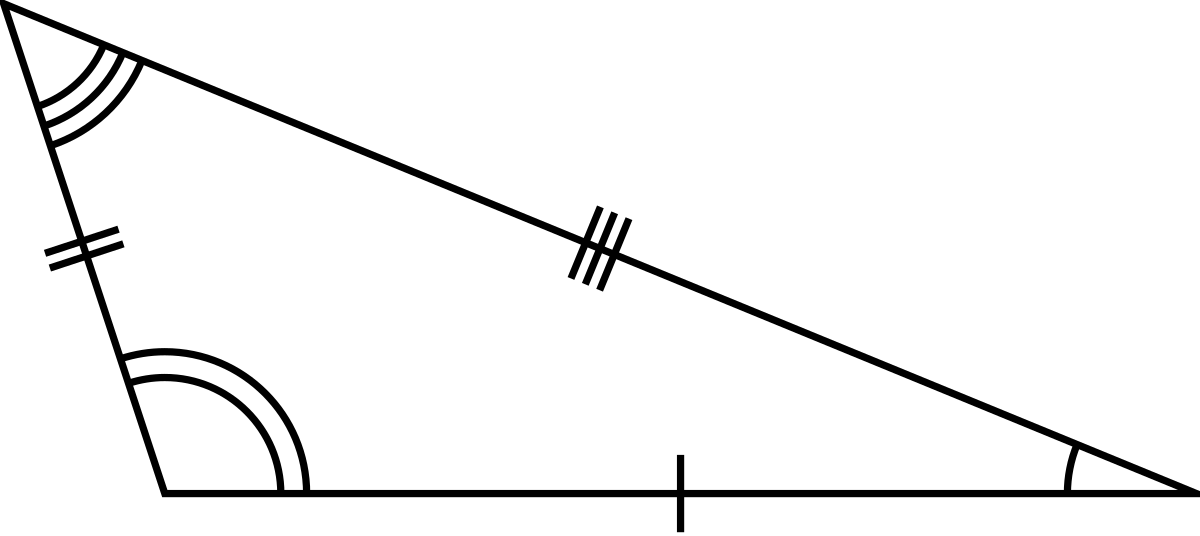



不等辺三角形 ウィクショナリー日本語版
三角比の値の求め方 「0,30,45,60,90,1,135,150,180度」 の三角比の値(単位円) sinθ,cosθ,tamθの関係式 (90°θ)の三角比の値; A Scalene Triangle(不等辺三角形) 不等辺三角形は、a scalene triangleと言います。Scaleneは、不等辺の、という意味です。 A scalene triangle has three unequal sides and three unequal angles (筆者訳)不等辺三角形は、3つの長さの異なる辺と3つの異なる角度を持つ。 出定義:凹関数(上に凸な関数) concave function 高橋『経済学とファイナンスのための数学』p67;
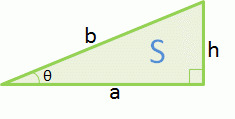



三角形の公式 Wakatta
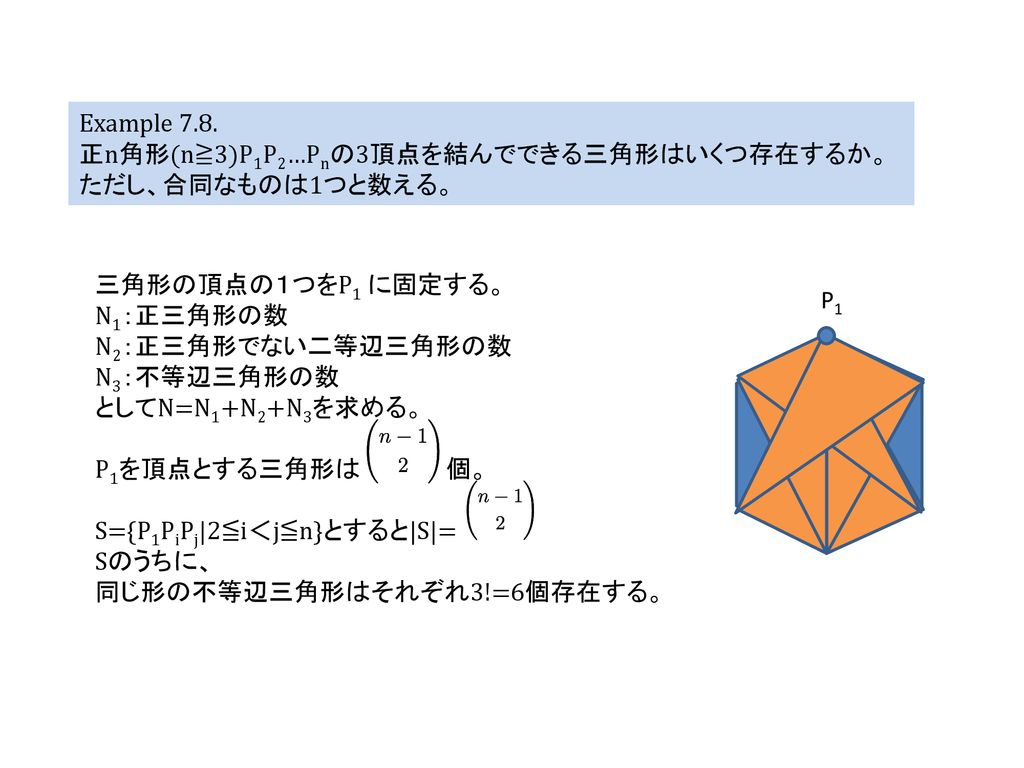



7章後半 M1 鈴木洋介 Ppt Download
③(不等辺三角形)と同じ仲間の図形を考える。 T これは仲間の学校です。しかし?がついていますが,何の仲間の学校なのか分かりません。この中には,③(不等辺三角形)が入ります。③と同じ仲間の図形はどれでしょう。 C どんな仲間なのかなあ。 C第2学年「長方形と正方形」では,三角形や四角形,直角,長方形,正方形,直角三角形 について,辺や頂点,角といった図形を構成する要素に着目し,図形の弁別をする。 定義や性質を理解するまでには至っていない。 不等辺四角形とスペシ プログラム クイズ 1.以下のプログラムを作ってみて下さい。 3つの整数を入力し、それを辺とする三角形が、正三角形、二等辺三角形、不等辺三角形のどれであるかを出力する。 例:3辺の長さを入力して
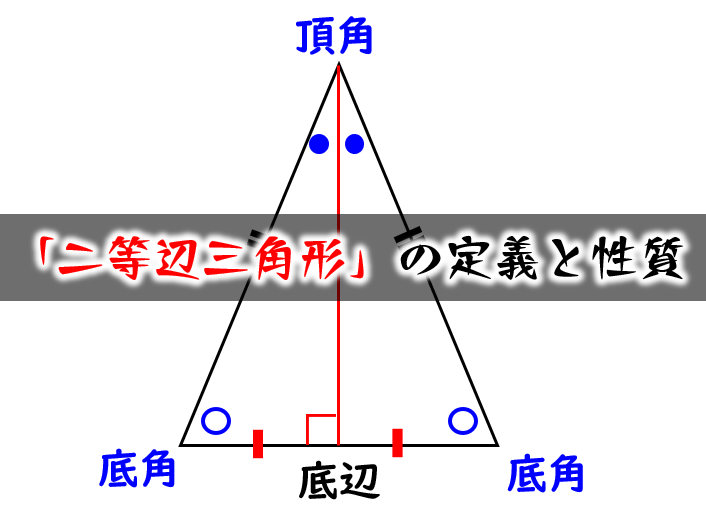



二等辺三角形の定義と性質 問題の解き方 数学fun



余弦定理
つまり,三角不等式を仮定すれば各変数が正であるという条件は自然に出てくるのです。 ・三角形の成立条件(存在条件とも言う)は 「三角形が存在するかどうか」を判定する条件 です。三角形の決定条件とは意味が異なるので注意して下さい。凸多角形の定義と認識方法 点列P=(p 0, p 1, p 2, , p n=p 0)が凸多角形を成すかどうかの判定: s ij 頂点p iとpjを結ぶ線分(対角線),ij≧2 仮定:多角形の辺は反時計回り(内部は辺の左)に順序付三角形の形状 本日のお題 ABC について,次の等式が成り立っているとき, ABC がどのような形状をしているかを考えましょう (1) a2 b2 = c2 (2) a2 − ab b2 = c2 (3) asinA bsinB = csinC (4) acosC = ccosA この等式を見て,三角形がどんな形をしているかを考えると



C言語入門 入力した3辺の長さから三角形の種類を判別 Webkaru




直角二等辺三角形 Wikiwand
鋭角三角形(えいかくさんかっけい、英 acute‐angled triangle )は、三角形の一種で、すべての角が直角 (90°=π/2 rad) よりも小さい図形である。 なお、鋭角三角形では、長辺をc、短辺をa,bとすれば、各辺は c 2 < a 2 b 2 の関係となり、また外心や垂心が三角形の内部に生ずる。 じすがなぼ まずは歌いましょう。wwwyoutubecom参考記事 三角形の五心の覚えておくべき性質を整理 高校数学の美しい物語 重心 三角形に対して、辺の中点をとする。辺, 辺についても同様に考えてを定義する。定理 直線は一点で交わる。この一点を重心という。三角形の3辺が与えられたときの面積の求め方 「3辺の長さが,5,4,7の三角形の面積を求めよ。」という問題がわかりません。面積を求めるときは,公式 S=1/2bc sinA に当てはめればいいことは二等辺三角形(にとうへんさんかくけい、英 isosceles triangle )



三角形 Wikipedia




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者
不等辺三角形は、すべての辺と角度が等しくない、つまり互いに異なることを特徴とする三角形です。 それはあなたに興味があるかもしれません: 不等辺三角形。 ジオメトリ。 角度に応じた三角形の種類 三角形は、直線(90°に等しい)の角度の幅に従っ(不等辺三角形 から転送) 出典 フリー百科事典『ウィキペディア(Wikipedia)』 ( 2335 UTC 版) 三角形(さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。



生花の概説



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典



中2数学 二等辺三角形の定義と性質 Examee




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強
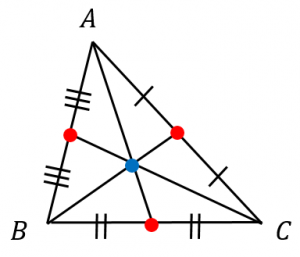



三角形の重心の定義といろいろな求め方 具体例で学ぶ数学
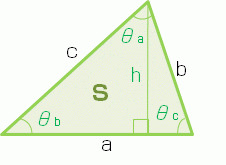



三角形の公式 Wakatta




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
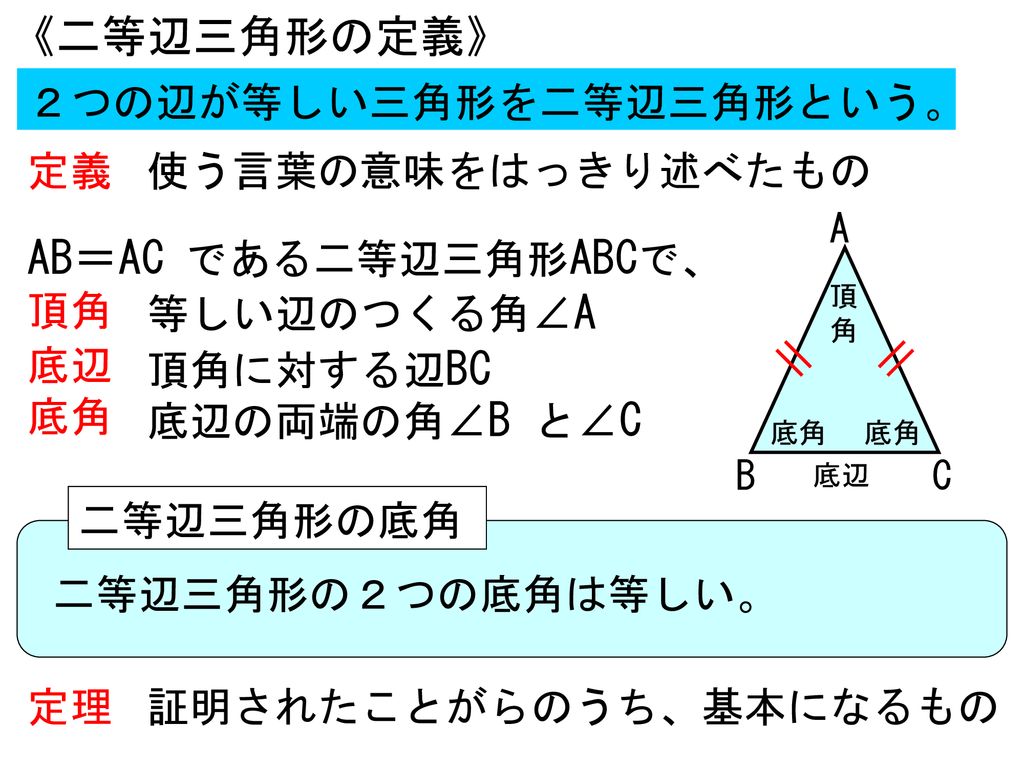



5 図形と合同 1章 三角形 1 二等辺三角形 4時間 Ppt Download




第1巻命題5 二等辺三角形の底角は等しい Stoixeia ストイケイア
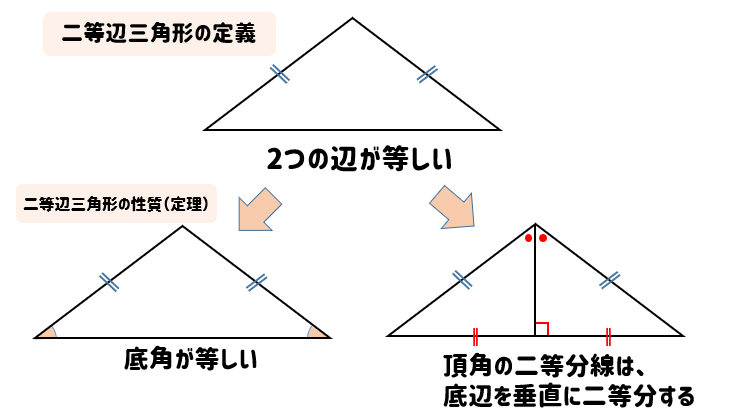



二等辺三角形の定義と性質をサクッと確認しておこう 数スタ




二等辺三角形の定義と性質 問題の解き方 数学fun




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強
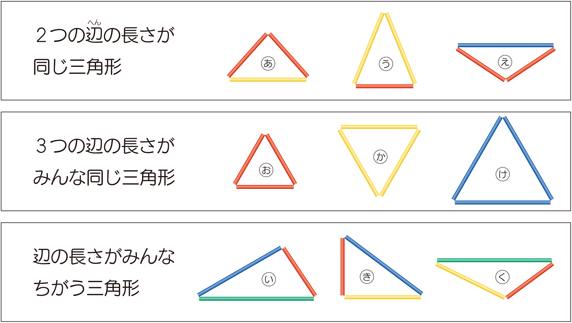



二等辺三角形と正三角形 算数用語集




二等辺三角形の性質 Youtube



ゆっるゆる アクアリウムと日本の庭園にみる伝統石組みレイアウト Mobi Aqua




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学
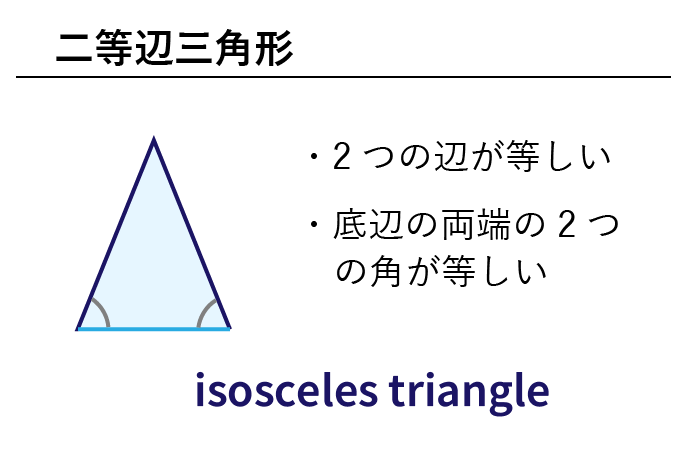



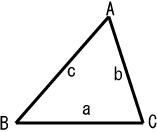
数学 色々な三角形の英単語まとめ 二等辺三角形 直角三角形ほか 英単語project




ビキニが似合う体型のポイント 不等辺三角形 とは Fitness Love
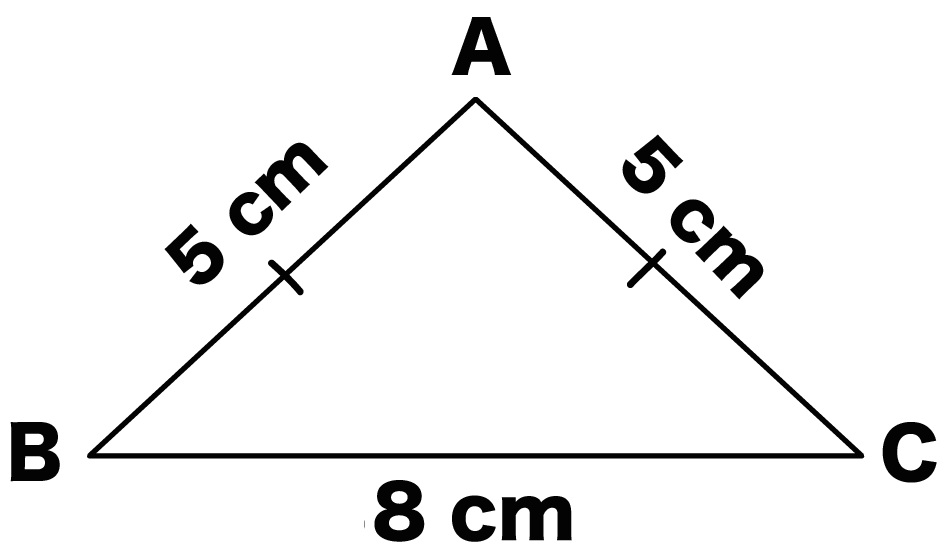



簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




マイヤーズの三角形問題 テストの基礎 Qbookアカデミー



ゆっるゆる アクアリウムと日本の庭園にみる伝統石組みレイアウト Mobi Aqua




不等辺三角形の定理 短編 麗人uno あがた愛 ボーイズラブマンガ Kindleストア Amazon




二等辺三角形 ゆるゆるプログラミング




不等辺三角形 至急ご回答お待ちしております 不等辺三角形について その他 学校 勉強 教えて Goo



二等辺三角形




二等辺三角形とは 一般の人気 最新記事を集めました はてな



10 樹形構想 初歩から学べる盆栽教室 盆栽 盆栽書籍 盆栽鉢の通販 近代出版




黄金三角形による18 シリーズの三角比 おいしい数学
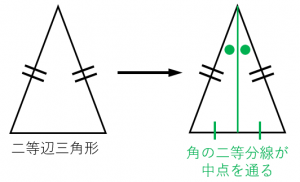



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学
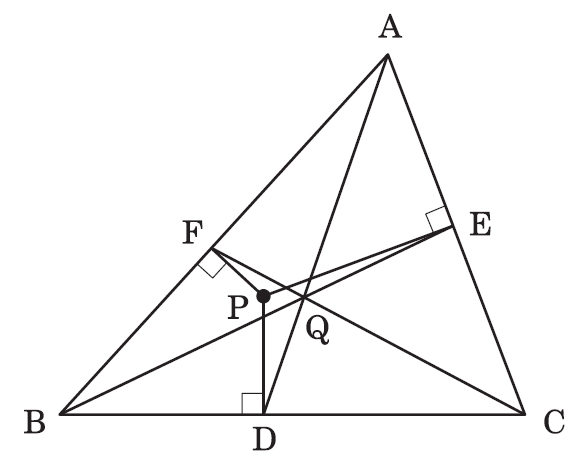



出題 年2月号掲載分 応募締切 2月8日 解答 年5月号掲載 Web日本評論



このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋




二等辺三角形の定義と定理 算数 数学が好きになりmath
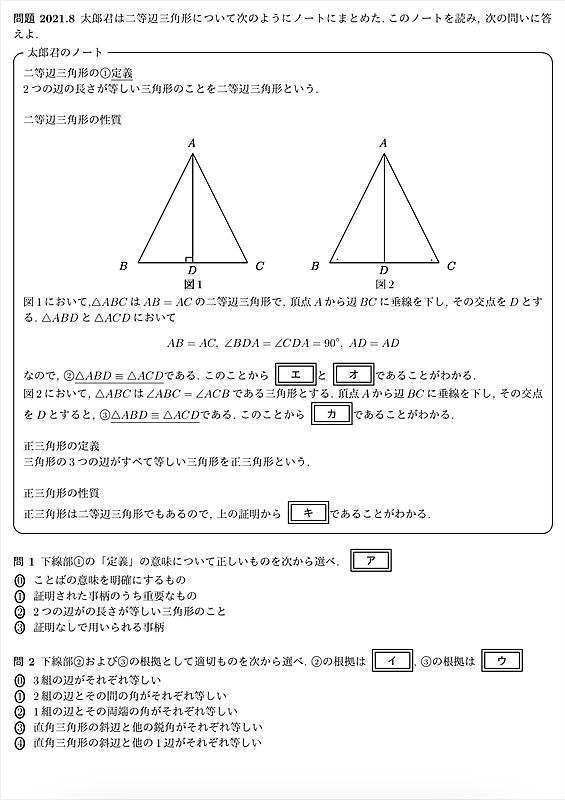



二等辺三角形とは 一般の人気 最新記事を集めました はてな
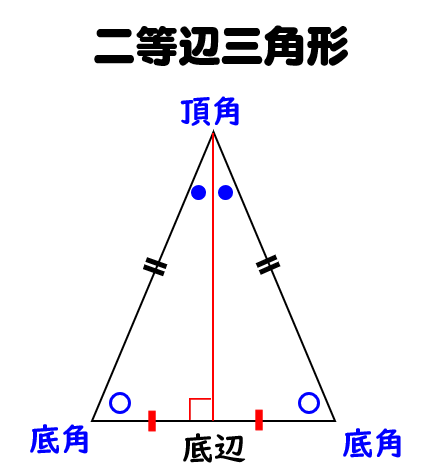



二等辺三角形の定義と性質 問題の解き方 数学fun




黄金三角形による18 シリーズの三角比 おいしい数学



このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋




15 号 形状認識システム 形状認識方法及び形状認識プログラム Astamuse




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット



99以上 不等辺三角形 辺の長さ 計算 不等辺三角形 辺の長さ 計算




三角形 Wikipedia




不等辺三角形の意味 用法を知る Astamuse



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める
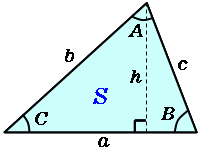



不等辺三角形 高精度計算サイト



二等辺三角形 三角形 図形 幾何 数学教育




不等辺三角形の意味 用法を知る Astamuse
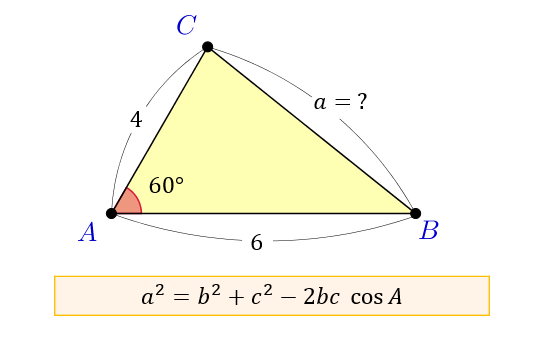



余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ
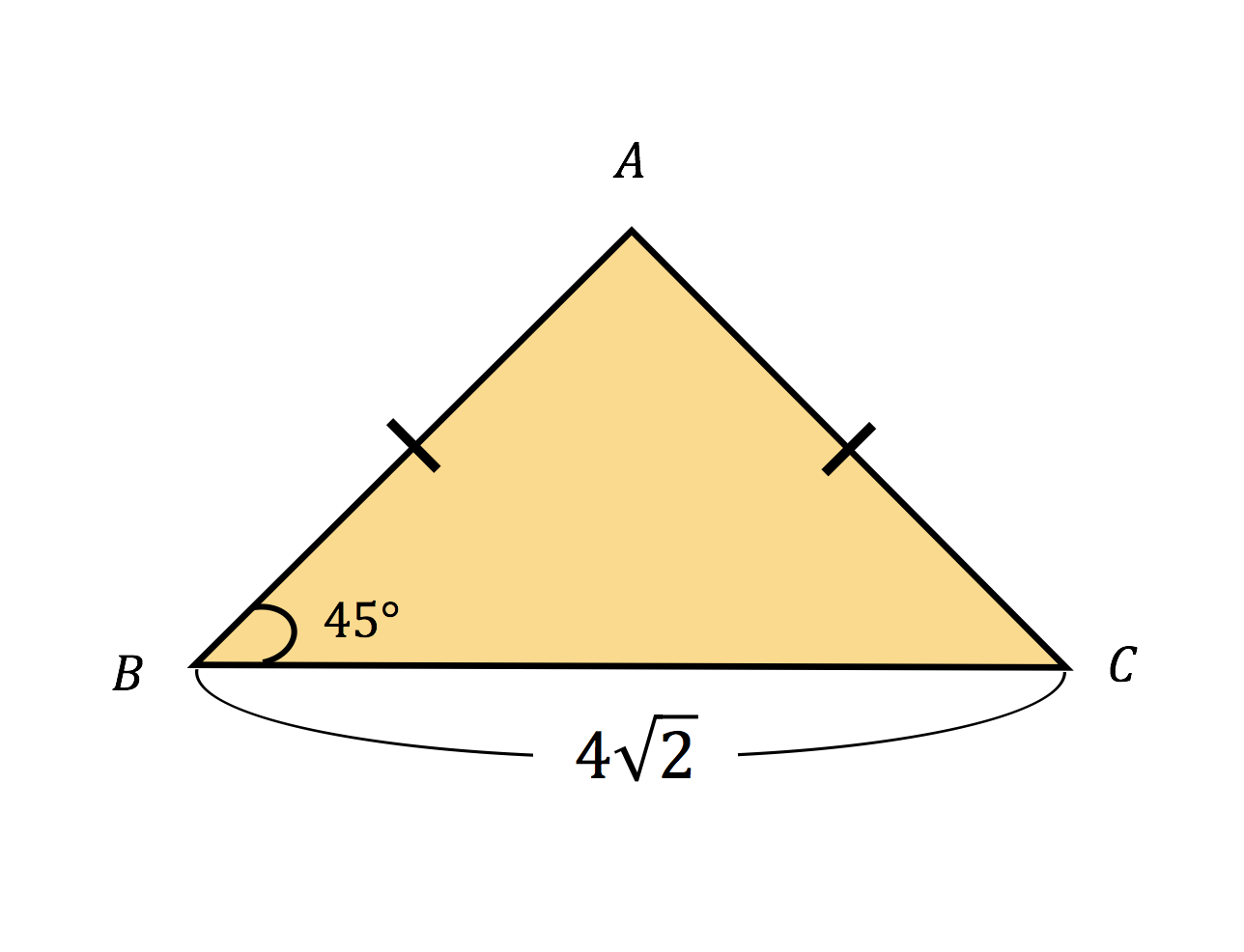



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ




二等辺三角形や直角三角形って英語で何て言うの 三角形の種類について 40代 50代 60代 シニア 初心者からやり直し英会話 英語学習法




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典



3



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学



3



二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係



台形と不等辺四角形 復氷




二等辺三角形 Wikipedia




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン



このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ




三角形




3 おかしな不等辺三角形 Imujii S Page



3年算数 三角形と角 の教え方




二等辺三角形の定義と性質 問題の解き方 数学fun




数学 中2 64 二等辺三角形 Youtube



11 7 数学 図形 これは 不等辺三角形 ふとうへんさんかっけい ですか 辺が揃ってない三角形の話 のっぽさんの勉強メモ




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ




二等辺三角形の底角は本当に等しいのか ひと筋縄ではいかない証明 ブルーバックス編集部 ブルーバックス 講談社 1 4




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ



3



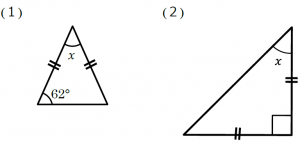
3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ
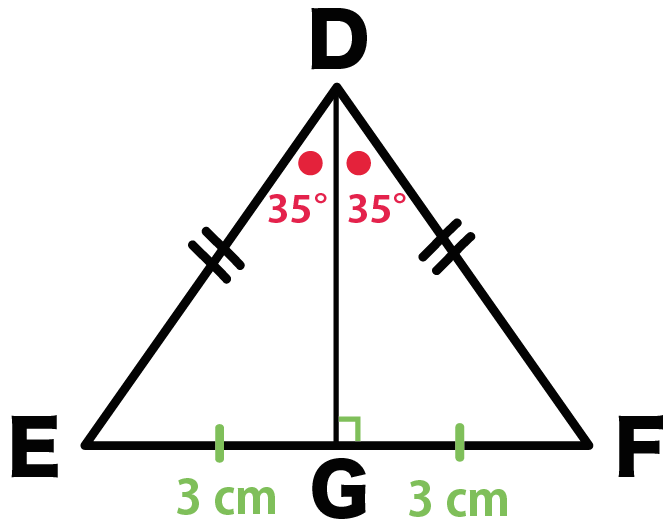



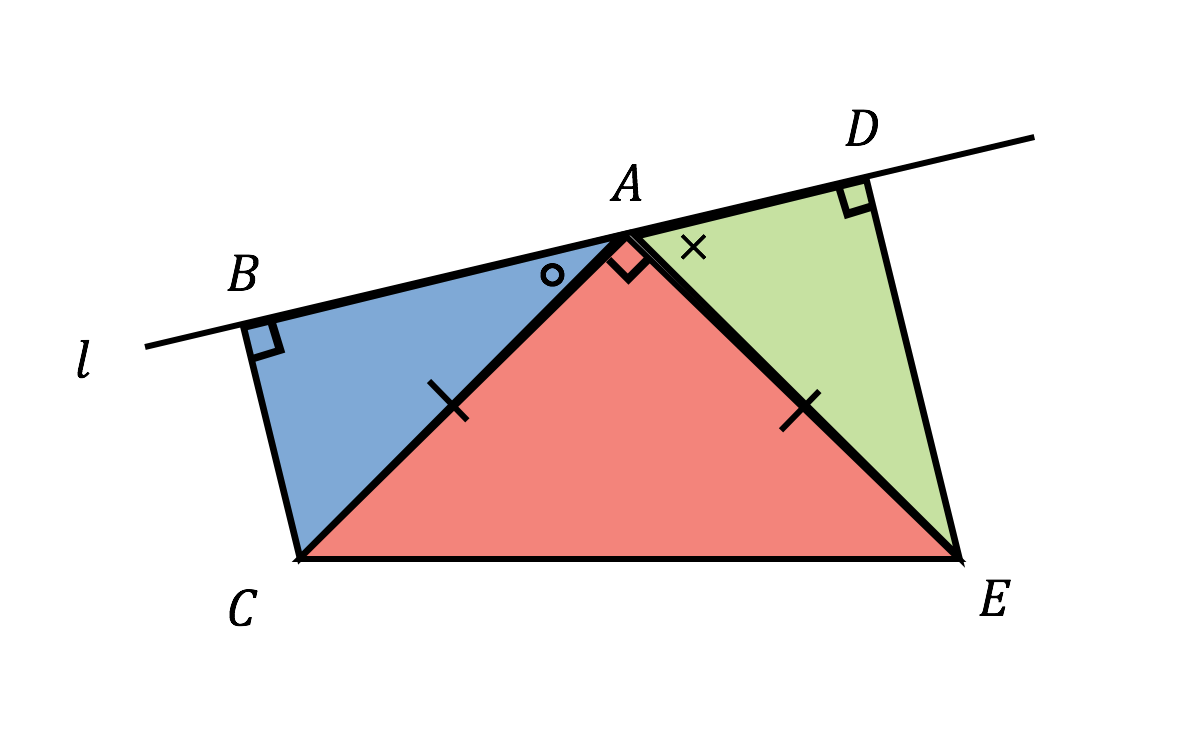
3分でわかる 二等辺三角形の2つの定理 性質 Qikeru 学びを楽しくわかりやすく



53 不等辺三角形的発想 庭語り どっとこむ エクステリアショップの未来創造集団
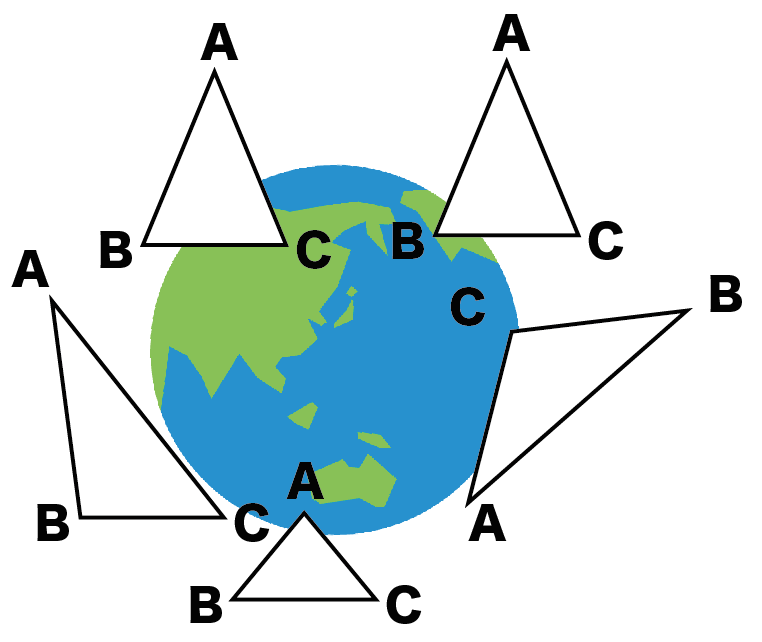



3分でわかる 二等辺三角形の定義 Qikeru 学びを楽しくわかりやすく
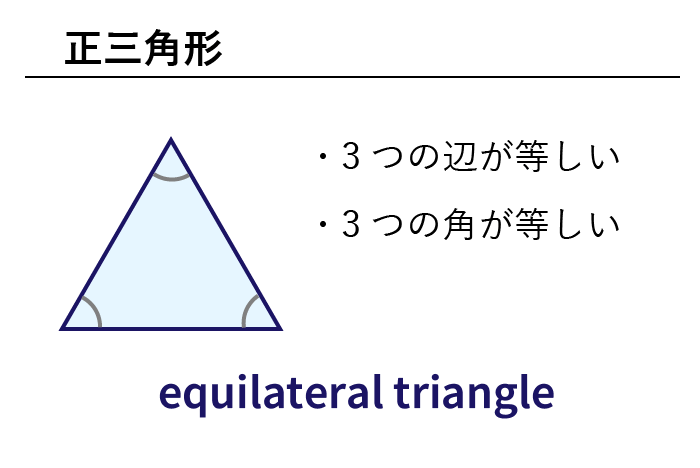



数学 色々な三角形の英単語まとめ 二等辺三角形 直角三角形ほか 英単語project
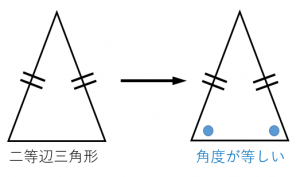



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学




二等辺三角形の定理や性質 底角が等しいことは絶対に覚えよう 中学や高校の数学の計算問題




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学
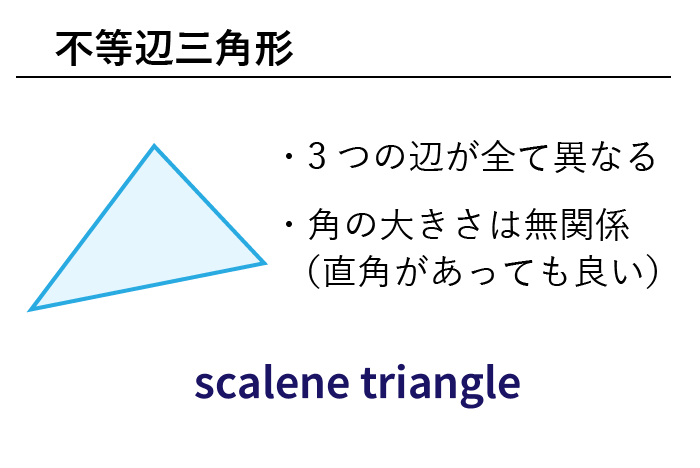



数学 色々な三角形の英単語まとめ 二等辺三角形 直角三角形ほか 英単語project




直角二等辺三角形 Wikipedia




余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ




直角三角形 Wikipedia




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ
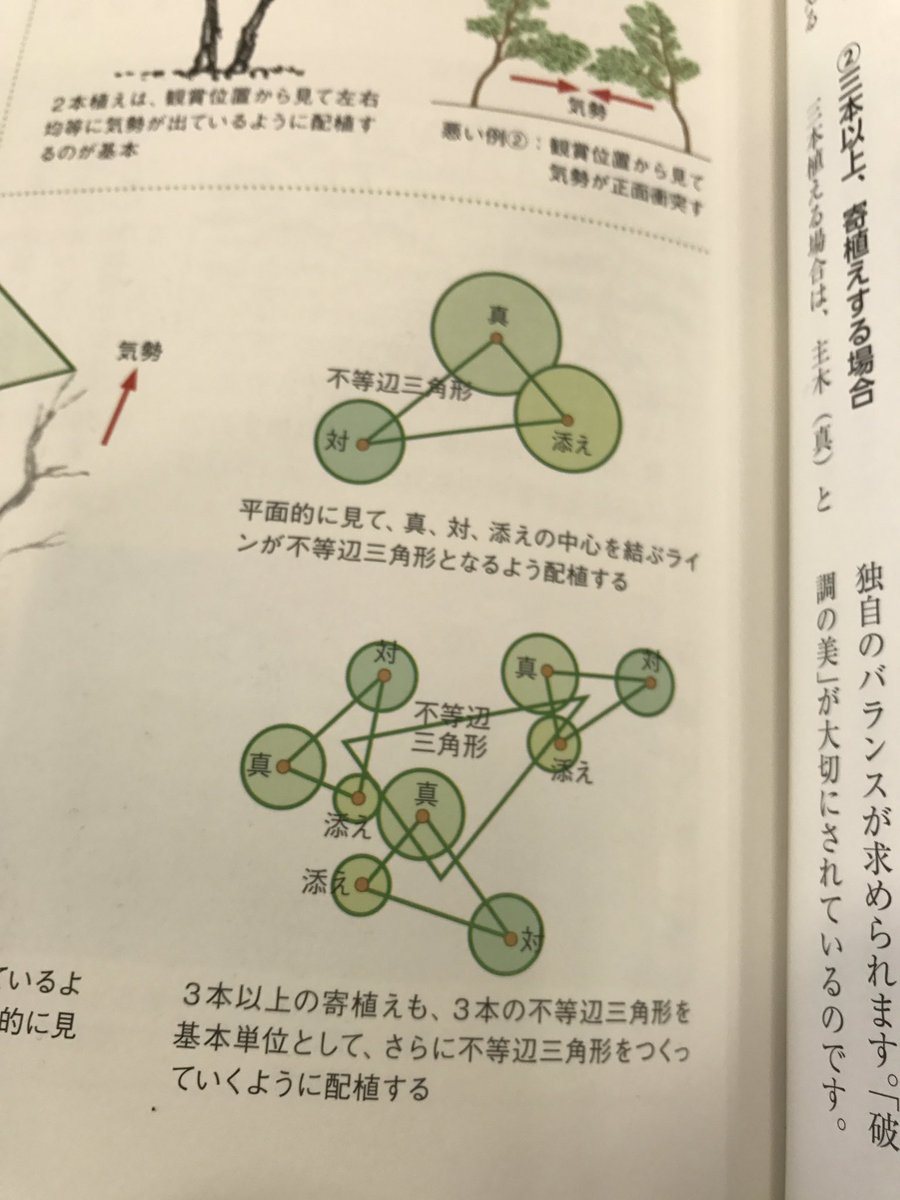



不等辺三角形のフラクタル 宇田川辰彦監修 庭師が教える 図解 日本庭園の見方 楽しみ方 勉強メモ Togetter



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典
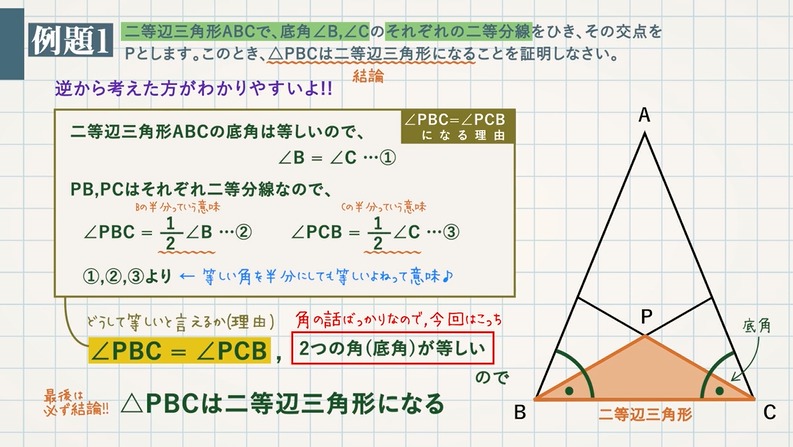



二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典
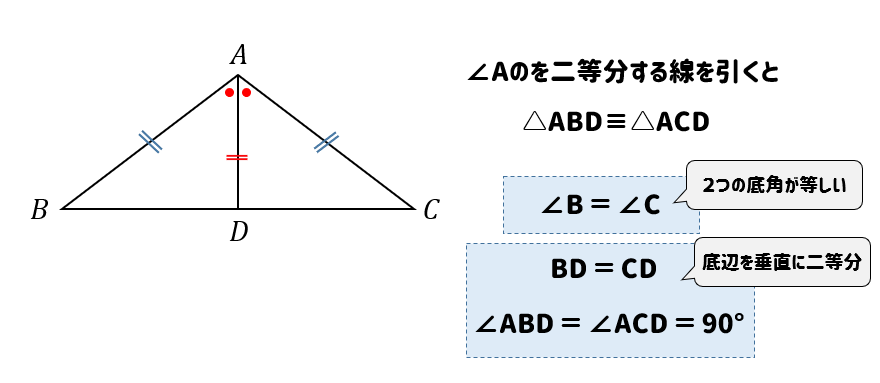



二等辺三角形の定義と性質をサクッと確認しておこう 数スタ




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ



0 件のコメント:
コメントを投稿